4. Kontextfreie Sprachen

Grammatiken und ihre Ableitungen

Grob gesprochen handelt es sich bei einer Grammatik um eine Menge von Regeln, die beschreiben, wie man aus einem Symbol durch das wiederholte Ersetzen von Teilwörtern ein Wort konstruieren kann.

Das Ersetzen eines Teilwortes durch ein anderes Teilwort nennt man in diesem Zusammenhang ableiten, und die Regeln, die vorgeben, welche Ersetzungen erlaubt sind, heißen Ableitungsregeln (oder Produktionsregeln). In einer kontextfreien Grammatik gibt es zwei Arten von Symbolen. Zum einen gibt es das Alphabet Σ welches die Zeichen enthält, die nicht weiter ersetzt werden können. Man nennt die Zeichen aus Σ auch Terminalsymbole.

Zum anderen gibt es die Zeichen, die noch zu ersetzen sind. Diese Zeichen nennen wir Variablen, und wir bezeichnen die Menge der Variablen mit V. Wir setzen voraus, dass V ∩ Σ = ∅.

Eine kontextfreie Grammatik G ist ein 4-Tupel G = 〈V, Σ, P, S〉 bestehend aus:

• V eine endliche Menge von Variablen
• Σ ein Alphabet, disjunkt zu V (d.h., Σ ∩ V = ∅)
• P eine Menge von Produktionsregeln der Form w → v für beliebige Wörter w und v über Σ ∪ V, wobei w mindestens eine Variable enthält (d.h. w, v ∈ (Σ ϵ V)∗ und w nicht-ϵ Σ∗)
• S eine Startvariable aus V (d.h. S ∈ V)

Das Anfangskellersymbol wird mit σ oder einem Dollarzeichen $ angegeben.

Die Elemente von Σ nennt man auch Terminalsymbole, die Elemente von V analog Nicht-Terminalsymbole oder Variablen. Die Menge aller Wörter, die sich von einer Grammatik G ableiten lassen, heißt die Sprache L dieser Grammatik.

Die Sprache einer kontextfreien Grammatik G = (V , Σ, P , S) ist definiert als L(G) := {w ∈ Σ∗ | S ⇒∗ w}

info

S ⇒* w bedeutet, dass aus dem Startsymbol S in null oder mehr Schritten das Wort w wird. Das ist also die reflexiv-transitive Hülle von ⇒

Kontextfreie Grammatiken und Kellerautomaten

Was sind und warum kontextfreie Grammatiken?

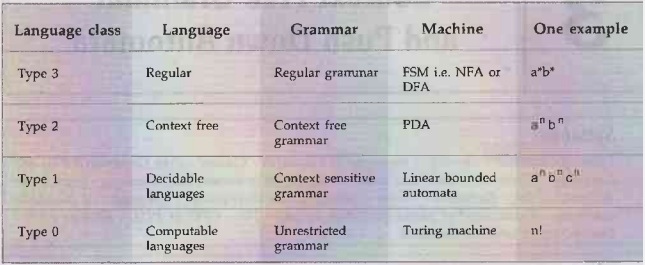
Ein DEA kann nicht prüfen, ob ein Wort zu einer nichtregulären-Sprache gehört. Zum Beispiel ist die Sprache L = {a^nb^n | n>=0} nicht regulär, denn diese enthält genau so viele as und bs und ein DEA kann die Zeichen nicht zählen, weil er keinen Speicher hat (sondern nur endlich viele Zustände). Eine solche Sprache nennen wir kontextfrei. „Kontextfrei“, weil ihre Produktionsregeln in der Grammatik nicht vom Kontext abhängen. Es bedeutet, dass die Position eines Nichtterminalsymbols (Symbol, das nicht in den endgültigen Wörtern der Sprache vorkommen) innerhalb eines Wortes irrelevant ist.

Jede reguläre (erkennbare) Sprache ist auch kontextfrei.

Kellerautomaten

Ein Kellerautomat ist ein NEA mit einem Kellerspeicher (stack). Im Keller können wir Zeichen ablegen, können aber immer nur auf das oberste Element (Top-Symbol) zugreifen. Das heißt, wir haben im Wesentlichen zwei Operationen: Mit einem Pop können wir das Top-Symbol des Kellers lesen und entfernen, mit einem Push können wir ein neues Element „auf“ dem Keller ablegen. Dieses neue Element ist dann das neue Top-Symbol.

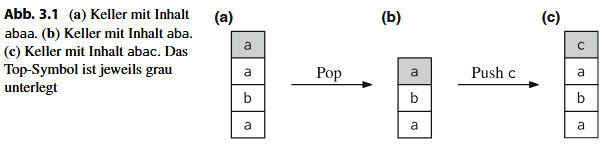
Ein Kellerautomat erkennt kontextfreie Sprachen. Kellerautomaten sind nichtdeterministisch aber es lässt sich auch eine deterministische Version davon ableiten (weniger mächtig, anders als bei DEAs/NEAs, die gleich mächtig sind).

Die Zustandsübergänge werden wieder durch eine Übergangsfunktion δ gesteuert. Ein Zustandsübergang hängt jedoch nun neben dem Eingabesymbol auch immer vom aktuellen Top-Symbol des Kellers ab. Außerdem ist das Ergebnis eines Zustandsübergangs nicht nur ein Folgezustand, sondern auch (möglicherweise) ein neues Top-Symbol.

Definition eines Kellerautomaten:

In Γ sind die Zeichen enthalten, die wir mit einem Push-Befehl im Keller abspeichern können. Die Übergangsfunktion ist so gewählt, dass sich mit ihr Push- und Pop-Befehle ausführen lassen. Es ist sogar möglich, ein Pop und ein Push hintereinander in einem Zustandsübergang ausführen zu lassen. Eine solche Doppelaktion tauscht also das Top-Symbol aus. Wir nennen diese Operation Switch.

Die Übergangsfunktion δ beschreibt die Befehle wie folgt: Wir übergeben der Funktion ein Tripel, bestehend aus dem aktuellen Zustand, dem aktuellen Eingabezeichen und dem aktuellen Top-Symbol. Das Eingabezeichen und das Top-Symbol kann hierbei aber auch ε sein. Die Übergangsfunktion gibt eine Menge von Paaren zurück, welche uns alle gültigen Übergänge angeben. Die Paare bestehen aus einem Folgezustand und einem neuen Top-Symbol. Wenn als Top-Symbol ein ε angegeben wird, heißt das, dass kein Push erfolgt. Auf diese Weise können wir einen Zustandsübergang inklusive eines Push-, Pop- oder Switchbefehls realisieren.

Beispiel:

δ(q, a, x) = {(p, ε)}: Wenn der aktuelle Zustand q, das nächste Zeichen der Eingabe ein a und das Top-Symbol ein x ist, können wir das a von der Eingabe lesen, in den Zustand p übergehen und das x als Top-Symbol entfernen. Dies entspricht einem Pop-Befehl.

Der Inhalt des Kellers besteht aus einer Folge von Zeichen aus Γ, also aus einem Wort aus Γ∗, wobei das Top-Symbol immer das letzte Zeichen (rechts) des Wortes ist. Um eine Berechnung fortführen zu können, müssen wir neben dem aktuellen Zustand auch den Kellerinhalt kennen. Ein Paar von Zustand und Kellerinhalt (p, s) mit p ∈ Q und s ∈ Γ∗ nennen wir eine Konfiguration eines Kellerautomaten. Die Funktion δ beschreibt die Überführung der Konfigurationen. Die Startkonfiguration ist gegeben durch (q0, ε), was heißt, dass unsere Berechnungen immer mit leerem Keller beginnen. Wir nennen eine Konfiguration (q, s) akzeptierend, falls q ∈ F .

Wir definieren nun die Sprache eines Kellerautomaten:

Mithilfe einer Grammatik können wir das Wortproblem (=gehört ein beliebiges Wort w zu einer kontextfreien Sprache L)

1-2 Beispiele aus 98-100 einfügen

Der Ableitungsbaum (Parse Tree)

Ein Ableitungsbaum soll dokumentieren, welche Regeln ausgeführt wurden, um ein Wort aus dem Startsymbol abzuleiten. Es ist ein weiteres Werkzeug neben der linearen Ableitung, wobei man die Struktur der Wörter besser erkennt.

Ein Ableitungsbaum ist ein geordneter Baum, was bedeutet, dass für jeden Elternknoten seine Kinder geordnet sind. Des Weiteren sind alle Knoten des Baumes beschriftet. Folgende Bedingungen muss ein Ableitungsbaum einer kontextfreien Grammatik G erfüllen:

• Alle inneren Knoten sind mit Variablen beschriftet, und in der Wurzel steht das Startsymbol.
• Alle Blätter sind mit Terminalsymbolen oder mit ε beschriftet.
• Wenn ein innerer Knoten die Beschriftung X aufweist und seine Kinder (von links nach rechts) mit x1, x2, . . . xk beschriftet sind, dann muss es in G die Regel X → x1x2 · · · xk geben.

Ein Ableitungsbaum zeigt, wie ein Wort durch Regelanwendungen entsteht. Die Eltern-Kind-Beziehungen repräsentieren dabei die verwendeten Produktionsregeln, und das Startsymbol steht als Wurzel ganz oben, weil es als Erstes ersetzt wird. Das endgültige Wort erhält man, indem man die Terminalsymbole der Blätter in Präorder, also in einer Tiefensuche von links nach rechts, aneinanderreiht. Im Unterschied zu einer linearen Ableitungssequenz macht ein Ableitungsbaum die Struktur und die Nebenläufigkeit der Regelanwendungen deutlicher sichtbar.

info

Die Tiefensuche ist eine Art, einen Baum zu durchlaufen. Man besucht zuerst den aktuellen Knoten (z. B. ein Nichtterminal), dann rekursiv seine Kinder von links nach rechts.

Nebenläufigkeit bedeutet, dass manche Teile des Ableitungsbaums unabhängig voneinander abgeleitet werden können. Zum Beispiel, wenn S → XY gilt, kann man X und Y „gleichzeitig“ weiter ableiten – ihre Reihenfolge spielt keine Rolle. Der Ableitungsbaum zeigt diese Parallelität viel besser als eine lineare Schritt-für-Schritt-Ableitung.

Kontextfreie Grammatiken für reguläre Sprachen

In der Regel erzeugen kontextfreie Grammatiken Sprachen, die nicht regulär sind. Aber es gibt eine spezielle Art der kontextfreien Grammatiken für reguläre Sprachen: rechtslineare Grammatiken.

Eine kontextfreie Grammatik heißt rechtslinear, falls alle rechten Seiten ihrer Regeln entweder aus einem Wort gebildet aus einem Terminal gefolgt von einer Variablen bestehen oder dem leeren Wort entsprechen.

Wir werden nun eine Methode beschreiben, wie man aus einer rechtslinearen Grammatik G = (V , Σ, P , S) einen NEA NG = (Q, Σ, δ, q0, F ) konstruieren kann, der die gleiche Sprache akzeptiert.

• Für die Zustandsmenge Q wählen wir Q = V .
• Für jede Regel X → aY ergänzen wir δ mit Y ∈ δ(X, a).
• Alle VariablenX, für die es die RegelX → ε gibt, wählen wir als akzeptierende Zustände.
• Der Startzustand ist q0 = S.

Beispiel:

S → aS | aA A → bA | aS | ε

Aus dieser Grammatik lässt sich ein NEA konstruieren:

Beweis Schulz S. 111

Es gilt auch, dass wir aus jeder regulären Sprache eine passende Grammatik finden können. Sei L eine reguläre Sprache und M = (Q, Σ, δ, q0, F ) ein DEA, welcher L akzeptiert. Wir definieren die Grammatik GM = (V , Σ, P , S) wie folgt:

• Als Variablen wählen wir die Zustände, das heißt V = Q.
• Für jeden Übergang δ(p, a) = q nehmen wir die Regel p → aq in P auf.
• Für jeden Zustand q ∈ F nehmen wir die Regel q → ε.
• Der Startzustand ist S = q0 .

Sei L eine reguläre Sprache, die von einem DEA M akzeptiert wird. Dann gibt es eine rechtslineare Grammatik GM mit L = L(GM ). Die Sprachen, die von rechtslinearen Grammatiken beschrieben werden, sind genau die regulären Sprachen.

Übungsaufgabe Schulz S. 112

Recherchieren

• Beispiele Ableitungsbäume Video
• Links- und Rechstlineare Gramamtiken
• Äquivalenz der Modelle Kellerautomat und kontextfreie Grammatik (nachlesen)

Chomsky-Normalform (CNF)

Kontextfreie Grammatiken erlauben es, dass auf den rechten Seiten der Regeln beliebige Wörter bestehend aus Terminalsymbolen und Variablen auftauchen. Nun zeigen wir, dass eine eingeschränkte Form der Ableitungsregeln ausreicht. Diese nennen wir die Chomsky-Normalform.

Warum ist die Normalform interessant?

Wenn wir eine Eigenschaft der kontextfreien Sprachen beweisen wollen, können wir auf die Sprache erzeugende kontextfreie Grammatik zurückgreifen. Wenn wir nun zusätzliche Annahmen über die Struktur der Regeln dieser Grammatik machen können, fällt es uns leichter, mit dieser Grammatik zu arbeiten. Sie ist übersichtlicher.

Definition der Chomsky-Normalform

Eine kontextfreie Grammatik G = (V , Σ, P , S) ist in Chomsky-Normalform (CNF), falls sie ausschließlich aus Regeln der folgenden Form besteht:

1. A → XY , wobei A, X und Y Variablen sind (möglicherweise identisch), X und Y sind jedoch nicht S
2. A → x, wobei A Variable und x Terminalsymbol
3. S → ε

Es gibt verschiedene Gründe, warum eine kontextfreie Grammatik nicht in CNF ist.

1. Es gibt Regeln, bei denen S auf der rechten Seite auftaucht.
2. Es gibt Regeln, bei denen die rechte Seite ε ist, die linke Seite jedoch nicht S.
3. Es gibt Regeln, bei denen die rechte Seite aus einer einzigen Variable besteht.
4. Es gibt Regeln, bei denen die rechte Seite mehr als 2 Zeichen lang ist.
5. Es gibt Regeln, bei denen die rechte Seite die Länge 2 hat und mindestens ein Terminalsymbol enthält.

Konvertierung einer Grammatik in die CNF (5 Schritte)

1. Wenn der Startsymbol S auf der rechten Seite befindet, erstellen wir ein neues Startsymbol S' mit entsprechend einer neuen Produktionsregel S' -> S
2. Alle Regeln der Form A -> ε entfernen (null productions) (s. unten)
3. Alle Regeln der Form A -> B entfernen (unit productions) (s. unten)
4. Alle Regeln mit langer rechter Seite A -> B1...Bn mit n > 2 mit A -> B1C mit C -> B2...Bn. Diesen Schritt muss wiederholt werden, bis alle Produktionsregeln nur zwei Symbole auf der rechten Seite haben.
5. Alle Regeln mit Termilansymbolen auf der rechten Seite entfernen, außer sie haben die erlaubte Form A -> a. Beispielsweise wird A -> aB mit A -> XB und X -> a

ε-Produktionen (null productions) entfernen

1. A -> ε zu entfernen, alle Produktionsregeln auffinden, bei denen die rechte Seite A enthält
2. In diesen Regeln alle As mit einem ε tauschen
3. Die resultierende Produktionsregeln in die Grammatik aufnehmen

Beispiel

S -> ABAC, A -> aA | ε, B -> bB | ε, C -> c

1. Bei A anfangen, weil die Regel auch ε produzieren kann.
2. In allen anderen Regeln, wo A auf der rechten Seite vorkommt, dieses A (ggf. einzeln) entfernen, z.B. bei S: S -> BAC | ABC | BC (hier wurde erst das erste, dann das zweite, dann beide As gleichzeitig entfernt)
3. Nun fügen wir die neu entstandenen Regeln in der Grammatik auf. Wichtig: die alten bleiben bestehen! Bei S: S -> ABAC | BAC | ABC | BC. Hier haben wir die ursprüngliche Regel + die drei neuen aus Schritt 2.

Lösung:

• S -> ABAC | ABC | BAC | BC | AAC | AC | C
• A -> aA | a
• B -> bB | b
• C -> c

Einheitsproduktionen (unit productions) entfernen

Einheitsproduktionen sind Produktionen der Form A -> B

1. Alle Regeln der Form A -> B identifizieren. Mit den gefundenen Regeln rechts Anfangen. Um A -> B zu entfernen, muss eine neue Regel A -> x erstellt werden, wobei B -> x in der Grammatik existiert und x ein Terminalsymbol ist.
2. A -> B entfernen
3. Mit allen im Schritt 1 identifizierten Regeln wiederholen
4. Unerreichbare Zustände entfernen

Beispiel

S -> XY, X -> a, Y -> Z|b, Z->M, M->N, N->a

Einheitsproduktionen sind: Y -> Z|b, Z->M, M->N. Wir fangen rechts mit M->Nan. Die Regel wird zu M->a, weil N->a produziert. Dasselbe wiederholen wir mit den anderen in Schritt 1 identifizierten Regeln.

Lösung:

• S -> AB
• A -> a|b
• B -> a|b
• C -> a (nicht erreichbar)
• D->a (nicht erreichbar)

Der CYK Algorithmus (COCKE, YOUNGER, KASAMI)

Das Wortproblem ist durch Kellerautomaten oder kontextfreie Grammatiken entscheidbar. Die nächste Frage ist, wie schnell es entscheidbar ist.

Der Algorithmus benutzt als Ausgangspunkt eine kontextfreie Grammatik G = (V , Σ, P , S) in Chomsky-Normalform.

Sei w das Wort, für welches wir entscheiden wollen, ob w ∈ L(G) oder w NICHT-∈ L(G). Die Länge von w bezeichnen wir mit n. Der CYK-Algorithmus versucht, das Wortproblem rekursiv zu lösen. Dazu werden wir w in Teilwörter teilen. Wir bezeichnen mit w[i, j] das Teilwort von w, welches mit dem i-ten Zeichen beginnt und mit dem j-ten Zeichen endet. Zum Beispiel beim Wort w abbab ist wi=aund wj=b.

In dieser Notation entspricht w[1, n] dem Wort w (1 = erstes Zeichen, n = letztes). Im CYK-Algorithmus werden die folgenden Mengen bestimmt Wi,j := {X ∈ V | X ⇒∗ w[i, j]}.

info

Wi,j ist die Menge aller Nichtterminale V, die das Teilstring w[i, j]. Aus X kann man durch eine Ableitung das Teilwort w[i,j].

Zu jeder kontextfreien Grammatik G in Chomsky-Normalform und zu jedem Wort w über dem Eingabealphabet entscheidet der algorithmus von COCKE, YOUNGER und KASAMI (kurz CYK-Algorihmus genannt) mit dem Zeitaufwand O(n3), ob w in der von G erzeugten Sprache liegt.

CYK-Algorithmus Vorgehen

Deterministische Kellerautomaten

Kontrollfragen

• Was bedeutet, dass eine kontextfreie Sprache unter bestimmten Operationen abgeschlossen ist?

Deterministische Kellerautomaten

Im Falle kontextfreier Sprachen gibt es die Äquivalenz zwischen deterministischen und nichtdeterministischen Kellerautomaten nicht. Die deterministischen Kellerautomaten akzeptieren eine echte Teilklasse kontextfreier Sprachen, die sogenannten deterministischen kontextfreien Sprachen. Es gibt also kontextfreie Sprachen, die von keinem deterministischen Kellerautomaten akzeptiert werden.

Deterministische kontextfreie Sprachen haben eine Reihe interessante Eigenschaften:

• Sie sind eindeutig: Jedem Wort einer solchen Sprache kann eindeutig eine Bedeutung (Semantik) zugeordnet werden, eine Eigenschaft, die für Programmiersprachen unerlässlich ist
• Wörter einer deterministischen kontextfreien Sprache können schnell, d.h. in linearer Zeit analysiert werden. Im Gegensatz dazu können Wörter nichtdeterministischer kontextfreier Sprachen mit dem CYK-Algorithmus nur in kubischer Zeit analysiert werden.

Definition eines deterministischen Kellerautomaten:

1. Regel: Jedes Tripel aus aktuellem Zustand (q), Eingabezeichen a und Topsymbol x darf höchstens einen (≤ 1)Zustandsübergang produzieren. Es gibt bei jeder Konfiguration nur eine Folgekonfiguration.
2. Regel: Die Maschine darf nicht gleichzeitig die Wahl haben, ein Zeichen zu lesen ODER einen Schritt ohne Lesen zu machen.

Die zweite Bedingung verbietet, dass für dieselbe Situation(gleicher Zustand, gleiches Topsymbol) beide Arten von Regeln (δ(q, a, x) oder δ(q, ε, x)) existieren.

Wegen dieser beiden Eigenschaften ist der Automat deterministisch.